[Data Structure] 시간 복잡도 (Time Complexity)

알고리즘 분석

알고리즘을 분석할 때는 다음의 세 가지 경우로 나눌 수 있다. 최악, 최선, 평균 의 경우

 

최악의 경우(Worst case)

프로그램이 실행시간의 상한을 계산한다.

프로그램이 실행될 때 연산이 수행되는 횟수가 최대가 되는 경우이다.

배열을 예로 들었을 때 탐색하려는 원소가 없거나 맨 끝에 위치한 경우이다.

 

최선의 경우(Best case)

프로그램 실행시간의 하한을 계산한다.

프로그램이 실행될 때 연산이 수행되는 횟수가 최소가 되는 경우이다.

배열을 예로 들었을 때 탐색하려는 원소가 맨 앞에 위치한 경우이다.

 

평균(Average case)

가능한 모든 입력(N)에 대한 실행 시간을 계산한 후, 모든 시간을 더한다.

더한 결과를 입력한 수(N)로 나눈다.

알고리즘 평가

알고리즘 평가하는 데 있어서 실행시간(연산 횟수)과 메모리 사용량을 평가기준으로 나눔

수행 시간(연산 횟수) : 시간 복잡도(Time Complexity)

메모리 사용량 : 공간 복잡도(Space Complexity)

시간 복잡도

시간 복잡도의 정의는 입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화한 것이다.

쉽게 풀이하자면 알고리즘이 문제를 해결하기 위한 연산의 횟수이다.

함수를 실행했을 때 함수의 수행 시간이 아닌 연산의 횟수를 센다.

 

알고리즘의 시간 복잡도는 주로 빅-오 표기법으로 나타낸다.

Big-O 표기법

계수와 낮은 차수의 항을 제외시키는 방법

 

f(n)	Name
1	Constant
log n	Logarithmic
n	Linear
n log n	Log Linear
n ^ 2	Quadratic
n ^ 3	Cubic
C ^ n	Exponential

성능 비교

O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^2) < O(2^n)

 

 

O(1) : Constant

알고리즘의 문제를 해결하는데 한 단계만 거침

값을 검색할 때 객체의 키를 알거나, 배열의 인덱스를 알고 있다면 언제나 한 단계만 걸림

1 ~ N까지의 합을 구하는 알고리즘을 구하기 위해 다음과 같은 공식을 사용할 수 있다.

공식 : N * (N+1) / 2

var N = 10
var sum = N * (N+1) / 2

sum		// 55

반복문을 사용해 하나씩 모두 더하는 알고리즘은 아래의 O(n)이다

 

O(log N) : Logarithmic

문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듦

ex, 효율 좋은 검색 알고리즘, 트리구조

 

O(N) : Linear

문제를 해결하기 위한 단계의 수와 입력받은 값 n 이 1:1의 관계를 가짐

1부터 N까지의 합을 구하기 위해 반복문을 사용해서 더하는 알고리즘 또한 구현할 수 있을 것이다.

var N = 10
var sum = 0
var count = 0

for(let i=1; i<=N; i++){
    sum += i
    count += 1
}

sum 	// 55
count 	// 10

1부터 10까지의 합을 구하는데 총 10번의 연산을 하였다

 

O(N log N) : Log Linear

ex, 효율 좋은 정렬 알고리즘

 

O(N^2) : Quadratic

문제 해결을 위한 단계의 수는 입력받은 값 n의 제곱

ex, 이중 루프

 

O(N^3) : Cubic

문제 해결을 위한 단계의 수는 입력받은 값 n의 세제곱

ex, 삼중 루프

 

O(C^N) : Exponential

문제 해결을 위한 단계의 수는 주어진 상수값 C의 n 제곱

 

 

그래프 시간 복잡도

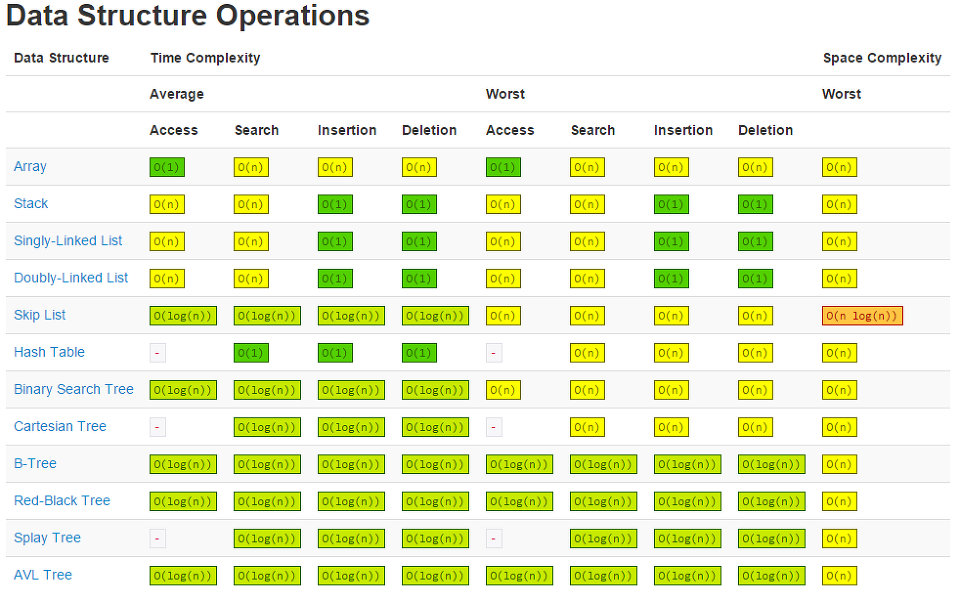
자료구조 시간 복잡도